A tangent line is just a line that touches the graph once. Here is a graph called f with a point labeled x and we calculate the slope of the tangent line at the point x with the difference quotient. The length from the origin to x is called "x." The coordinates at that point x (that is touching the tangent line) is (x,f(x)). Another point to the right of x is called "h(delta x or change in x)". So this new point has the coordinates of (x+h,f(x+h)). A secant line is a line that goes through two points. To find the slope of the secant line you need to use the point slope formula, which is y2-y1/x2-x1. Then, you just plug in the x and y values and you get f(x+h)-f(x)/ x+h-x. The x's will cancel in the denominator and you are left with f of x plus h minus f of x divided by h that's the difference quotient! So the difference quotient represents the slope of the secant line. The smaller the change in x, the more the secant line resembles the tangent line. To make the change in delta x smaller we use a limit in the secant slope. So we take the limit as h(delta x) approaches 0 because we want our delta x to be as small as possible for the secant line to resemble the tangent line. We can take the limit as h approaches 0 because approaches means getting close, but never getting there and that's exactly what we need (to get close to zero but not zero because we can't have 0 in our denominator). The difference quotient is the definition of the derivative.
Math is everywhere
Tuesday, June 3, 2014
Monday, May 12, 2014
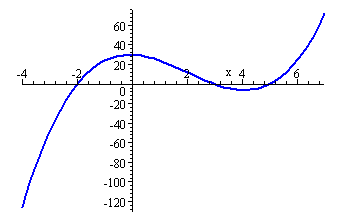
BQ#6 Unit U Concept 4:Continuous functions and types of discontinuities and limits numerically and graphically
1. A continuous function is predictable. It has no breaks, no holes, and no jumps. A continuous function can be drawn with a single, unbroken pencil stroke. Also, a continuous function is when the value is equal to the limit.
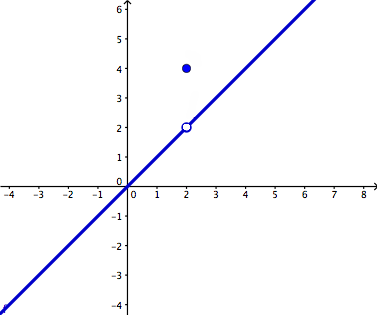
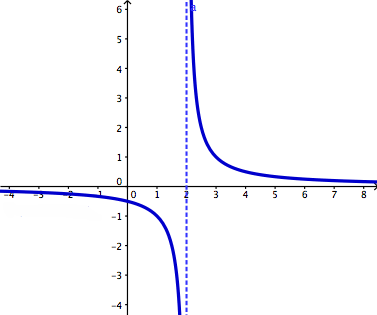
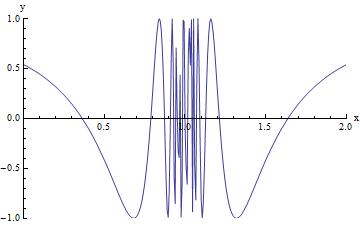
A discontinuous function is the opposite of a continuous function. It may contain breaks, holes, jumps. Also, the value does not equal the limit. There are two families of discontinuities: removable and non-removable discontinuities. In the removable family there is only point discontinuity. In removable discontinuities the limit DOES EXIST. In the other family, non-removable discontinuities the limit DOES NOT EXIST. The non-removable discontinuities family consists of jump discontinuity, oscillating behavior, and infinite discontinuity. In the jump discontinuities one hole has to be close and one open or both open or it will not be a function if both of the holes are closed. The reason the limit does not exist in jump discontinuities is because it approaches different values from the left and right. In oscillating behavior the graph is very wiggly and the limit does not exist because it doesn't approach any single value. Infinite discontinuities are caused by vertical asymptotes and the limit does not exist because of unbounded behavior (can't touch asymptotes) and because it approaches different values from the left and right.
2. A limit is the intended height of a function. The height is just the y-value of the function. Different x-values have different heights. A limit exists as long as you reach the same height from both the left and right. In order for a limit to exist, both the right hand limit and the left hand limit must be the same. If a graph does not break at a given x-value, a limit exists there. A limit can still exist if the destination is a hole in the graph. A graph can have an infinite amount of limits. Limits do not exist at specific points in the three non-removable discontinuities-jump, infinite, and oscillating. The limit does not exist at jump discontinuities because it approaches different values from the left and right. The limit does exist at infinite discontinuities because of unbounded behavior (can't touch asymptotes) and it approaches different values from the left and right. The limit does exist at oscillating behavior because it does not approach any single value because infinity is not anything you can get to. The difference between a limit and a value is the actuality. A limit is the intended height, while a value is the actual height.
3.We evaluate limits numerically by typing in the given function into out y= screen in our graphing calculator. Then, pressing the graph button and then hitting the trace button and we put in the number that we given in the table and repeat for all the others. On the left side of the table the number should increase from out to inner and on the right side of the table the number should increase out to inner. Then, you write out the number that is the middle or what the numbers are approaching and that number will become the limit. After, that you just write it as limit notation. We evaluate limits graphically by putting your finger on a spot to the left and to the right of where you want to evaluate the limit. If your fingers meet up then that y-value will be you limit. If your fingers do not meet up, the limit does not exist. The possible reasons for why the limit does not exist is because different values from the left and right, unbounded behavior, and oscillating behavior.We can evaluate limits algebraically by using three different methods. The first method, is substitution which is the easiest way to go about and we should always try to see if we get a numerical value, #/0(undefined= LIMIT DNE because unbounded behavior),and 0/#(limit is zero). If we ever get 0/0 when using the substitution method that means it is indeterminate, which means not yet determined and we must use another method. The substitution method means you take the number limit is approaching and plug it anytime you see "x". The second method, is factoring we use this method when the substitution method gives us 0/0 and the numerator or denominator are factorable. When using the factoring method we factor the numerator and denominator and cancel common terms to remove the zero(hole) in the denominator and then we use direct substitution method to get the limit. The last method is the conjugate method, we use this when the substitution method gives us 0/0 and the numerator or the demoniator are not factorable. We evaluate the limit using the conjugate method by first multiplying the top and bottom by the conjugate of the numerator or denominator(we use the conjugate of the numerator/denominator depending wherever the radical is). Then we simplify by foiling(you don't multiply the non-conjugate part because you want things to cancel) and then things will cancel and then we use the substitution method.
 | |||||||||
| http://www.intmath.com/differentiation/1-limits-and-differentiation.php |
 | |
| http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity |
 |
| http://www.tutorvista.com/content/math/discontinuity/ |
 |
| http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity |
 |
| http://www.cwladis.com/math301/limitsgraphically.php |
3.We evaluate limits numerically by typing in the given function into out y= screen in our graphing calculator. Then, pressing the graph button and then hitting the trace button and we put in the number that we given in the table and repeat for all the others. On the left side of the table the number should increase from out to inner and on the right side of the table the number should increase out to inner. Then, you write out the number that is the middle or what the numbers are approaching and that number will become the limit. After, that you just write it as limit notation. We evaluate limits graphically by putting your finger on a spot to the left and to the right of where you want to evaluate the limit. If your fingers meet up then that y-value will be you limit. If your fingers do not meet up, the limit does not exist. The possible reasons for why the limit does not exist is because different values from the left and right, unbounded behavior, and oscillating behavior.We can evaluate limits algebraically by using three different methods. The first method, is substitution which is the easiest way to go about and we should always try to see if we get a numerical value, #/0(undefined= LIMIT DNE because unbounded behavior),and 0/#(limit is zero). If we ever get 0/0 when using the substitution method that means it is indeterminate, which means not yet determined and we must use another method. The substitution method means you take the number limit is approaching and plug it anytime you see "x". The second method, is factoring we use this method when the substitution method gives us 0/0 and the numerator or denominator are factorable. When using the factoring method we factor the numerator and denominator and cancel common terms to remove the zero(hole) in the denominator and then we use direct substitution method to get the limit. The last method is the conjugate method, we use this when the substitution method gives us 0/0 and the numerator or the demoniator are not factorable. We evaluate the limit using the conjugate method by first multiplying the top and bottom by the conjugate of the numerator or denominator(we use the conjugate of the numerator/denominator depending wherever the radical is). Then we simplify by foiling(you don't multiply the non-conjugate part because you want things to cancel) and then things will cancel and then we use the substitution method.
Friday, April 18, 2014
BQ#4 Unit T Concept 1-3: Graphing all six trig functions
A normal tangent is uphill and a normal cotangent is downhill because of the placement of the asymptotes. For tan it goes uphill because we have asymptotes where cos equals zero(since tan's trig identity is sin/cos and we need to have zero in the denominator to get undefined=asymptotes) and remembering that we need to be in between the asymptotes but not touch them and tan needing to be positive in the first quadrant (because the sin and cos graphs being positive in quadrant one and a positive divided by a positive is positive=tan ) and tan needing to be negative in quadrant two, uphill is the only way you can fit the graph in between the asymptotes. For cot it goes downhill because we have asymptotes when sin equals zero(cot=cos/sin). Cot needs to be positive in the first quadrant(sin and cos are both positive) and negative in quadrant two(sin is postive and cos is negative; positive divided by a negative=negative) and downhill is the only way we can fit the graph in between the asymptotes and it be positive and negative in the second quadrant. To bring it all together the placement of the asymptotes makes a normal tangent uphill and a cotangent downhill.
BQ#3 Unit T Concept 1: Graphing all six trig functions
A.) Once, we draw the sin and cos graphs(sin graph starting and ending at 0 and cos graph starting and ending in its amplitude), we notice that the sin and cos graph are both positive in quadrant one, so the tangent graph is positive because if tan is sin/cos and sin and cos are positive a positive divided by a positive is positive.In quadrant two, the sin graph is positive and the cos graph is negative, so the tan graph is negative because a positive divided by a negative is negative. In quadrant three, the both the sin and cos graph are negative therefore the tan graph is positive because a negative divided by a negative is a positive. In quadrant four, sin is negative and cos is positive, so the tan graph is going to be negative. Tangent has an asymptote whenever cos equals zero. The asymptotes are determined with sin and cos. Asymptotes happen when we get undefined. We get undefined when we divide by zero or when cos is zero because tan is sin/cos.
B.)We know cot is cos/sin by our trig identities. Looking at quadrant one, we noticed both the sin and cos graphs are positive, so the cot graph will be positive. Cotangent is going to have different locations for asymptotes as opposed to tangent.Cotangent is going to have asymptotes whenever sin equals one. In quadrant two, sin is positive, but cos is negative so the cot graph will be negative. In quadrant three, both sin and cos are negative so cotangent is going to be positive. In quadrant four, cos is positive and sin is negative so cotangent will be negative.The asymptotes are determined with sin and cos.Asymptotes happen when we get undefined. We get undefined when we divide by zero or when sin is zero because cot is cos/sin.
C.)Secant is the reciprocal of cosine. In quadrant one, secant is positive and it goes very high up because if you take the reciprocal of a small fraction you will get a really big number. Sec is going to have asymptotes whenever cos equals zero.In quadrant two, cos is negative so sec is going to be negative because it needs to reflect off from the cos graph. In quadrant three, cos is negative, so sec is negative. In quadrant four, cos is positive so sec is positive.
D.)When sin equals zero there is going to be asymptotes. In quadrant one and two, sin is positive so csc is going to be positive or above the x-axis because it reflects off the sin graph.In quadrant three and four, sin is negative so csc will be negative or below the x-axis. The location of the asymptote shapes our graph. We have asymptotes when we get undefined and if we look at csc trig identity it is is 1/sin so sin has to be zero in order for us to get undefined which means asymptotes.
B.)We know cot is cos/sin by our trig identities. Looking at quadrant one, we noticed both the sin and cos graphs are positive, so the cot graph will be positive. Cotangent is going to have different locations for asymptotes as opposed to tangent.Cotangent is going to have asymptotes whenever sin equals one. In quadrant two, sin is positive, but cos is negative so the cot graph will be negative. In quadrant three, both sin and cos are negative so cotangent is going to be positive. In quadrant four, cos is positive and sin is negative so cotangent will be negative.The asymptotes are determined with sin and cos.Asymptotes happen when we get undefined. We get undefined when we divide by zero or when sin is zero because cot is cos/sin.
C.)Secant is the reciprocal of cosine. In quadrant one, secant is positive and it goes very high up because if you take the reciprocal of a small fraction you will get a really big number. Sec is going to have asymptotes whenever cos equals zero.In quadrant two, cos is negative so sec is going to be negative because it needs to reflect off from the cos graph. In quadrant three, cos is negative, so sec is negative. In quadrant four, cos is positive so sec is positive.
D.)When sin equals zero there is going to be asymptotes. In quadrant one and two, sin is positive so csc is going to be positive or above the x-axis because it reflects off the sin graph.In quadrant three and four, sin is negative so csc will be negative or below the x-axis. The location of the asymptote shapes our graph. We have asymptotes when we get undefined and if we look at csc trig identity it is is 1/sin so sin has to be zero in order for us to get undefined which means asymptotes.
Thursday, April 17, 2014
BQ#5 Unit T Concept 1-3: Graphing all six trig functions
To begin with, the Unit Circle ratios for sin is y/r, cos is x/r, csc is r/y( because it is the reciprocal of sine), sec is r/x(because it is the reciprocal of cos), tan is y/x, and cot is x/y (because it is the reciprocal of tan). With that being said, we have amplitudes when we are dividing by zero, which will give us defined because we can't divide by zero. Sin and cos never have asymptotes because if we look at their Unit Circle ratios, r is always in the denominator. As we know when we are dealing with the Unit Circle, r is always 1. Therefore, we never divide by zero, which we do not have amplitudes because it is never undefined because we do not divide by zero.
Wednesday, April 16, 2014
BQ#2: Unit T Concept Intro: Graphing all six trig functions
Trig graphs relate to the Unit Circle because if we took the Unit Circle and unwrapped it, it will become a straight line and the four quadrants will become hash marks.
A.)So, for sine and cosine the period is 2 pi because sine's pattern is ++-- and cosine's pattern is +--+(based on All Students Take Calculus) and looking at these patterns it will take the whole rotation of the Unit Circle or all of the four quadrants for the pattern to begin to repeat itself. If we look at the Unit Circle half way at 180 degrees it is pi and at 360 degrees (which is all the way around) it will be 2pi and since it takes sine's and cosine's pattern to begin repeating itself after four quadrants, which is at 360 degrees and 360 degrees is 2pi. One time through their cycle is called a period and therefore sine and cosine have periods of 2pi. On the other hand, tangent and cotangent have periods of pi(180 degrees) because tan's and cot's pattern is +-+- and as you can see the pattern is repeated twice. So, after two quadrants(180 degrees) the period starts to repeat itself therefore it is pi, instead of 2pi.
B.)Knowing the fact that sin and cos have to be in between 1 and -1 and that the Unit Circle can extend (0,1 at 90 degrees), (0,-1 at 270 degrees), (1,0 at 0 and 360 degrees), and (-1,0 at 180 degrees) we can state that sine and cosine have amplitudes of one. Also, sin and cos both have r=1 as a denominator.
A.)So, for sine and cosine the period is 2 pi because sine's pattern is ++-- and cosine's pattern is +--+(based on All Students Take Calculus) and looking at these patterns it will take the whole rotation of the Unit Circle or all of the four quadrants for the pattern to begin to repeat itself. If we look at the Unit Circle half way at 180 degrees it is pi and at 360 degrees (which is all the way around) it will be 2pi and since it takes sine's and cosine's pattern to begin repeating itself after four quadrants, which is at 360 degrees and 360 degrees is 2pi. One time through their cycle is called a period and therefore sine and cosine have periods of 2pi. On the other hand, tangent and cotangent have periods of pi(180 degrees) because tan's and cot's pattern is +-+- and as you can see the pattern is repeated twice. So, after two quadrants(180 degrees) the period starts to repeat itself therefore it is pi, instead of 2pi.
B.)Knowing the fact that sin and cos have to be in between 1 and -1 and that the Unit Circle can extend (0,1 at 90 degrees), (0,-1 at 270 degrees), (1,0 at 0 and 360 degrees), and (-1,0 at 180 degrees) we can state that sine and cosine have amplitudes of one. Also, sin and cos both have r=1 as a denominator.
Wednesday, April 2, 2014
Reflection#1: Unit Q: Verifying Trig Identities
1.) To verify trig functions it means to prove that the equation on the right is true by showing that the left side equals to the right. In other words, taking an equation and simplifying it until it is exactly the same as the right side. Verifying trig functions can be challenging because there is no set or "correct" method to verify these trig function and all it comes down is to a pick and guess situation and if it takes you to a more difficult path, then you can reverse and try another method.
2.) The number one tip I could give is listen to Mrs. Kirch when she says that you need to study in order to remember all the trig ratios, identities, and Pythagorean identities. The most helpful trick I can give is if you are stuck and you can get things to be converted into sin and cos then you should take that route. Another, tip I can give is to substitute the variables into something that is different from all the sin, pluses, minuses,etc. because a + next to a tan can be confusing.
3.)When verifying trig functions the first thing that I think is can I take out a GCF. If I can then you might want to do that first because perhaps things start cancelling out right there and then. The next step I take is to see if I can substitute an identity. It can be one of the ratio identities, reciprocal identities, or Pythagorean identities. Then, I look if the denominator is a binomial and if it is I can multiply by the conjugate to the numerator and denominator. Another thing you can perform is to combine fractions with binomial denominator or separate fraction, but only when the denominator is a monomial. In addition, you can factor and if all fails you can resort to changing everything to sin and cos.
2.) The number one tip I could give is listen to Mrs. Kirch when she says that you need to study in order to remember all the trig ratios, identities, and Pythagorean identities. The most helpful trick I can give is if you are stuck and you can get things to be converted into sin and cos then you should take that route. Another, tip I can give is to substitute the variables into something that is different from all the sin, pluses, minuses,etc. because a + next to a tan can be confusing.
3.)When verifying trig functions the first thing that I think is can I take out a GCF. If I can then you might want to do that first because perhaps things start cancelling out right there and then. The next step I take is to see if I can substitute an identity. It can be one of the ratio identities, reciprocal identities, or Pythagorean identities. Then, I look if the denominator is a binomial and if it is I can multiply by the conjugate to the numerator and denominator. Another thing you can perform is to combine fractions with binomial denominator or separate fraction, but only when the denominator is a monomial. In addition, you can factor and if all fails you can resort to changing everything to sin and cos.
Subscribe to:
Posts (Atom)
