BQ#6 Unit U Concept 4:Continuous functions and types of discontinuities and limits numerically and graphically

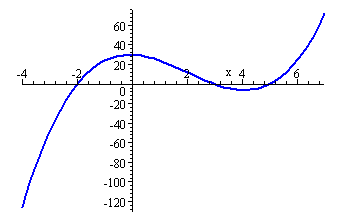
1. A continuous function is predictable. It has no breaks, no holes, and no jumps. A continuous function can be drawn with a single, unbroken pencil stroke. Also, a continuous function is when the value is equal to the limit.

http://www.intmath.com/differentiation/1-limits-and-differentiation.php

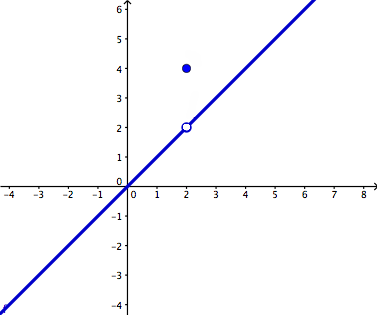
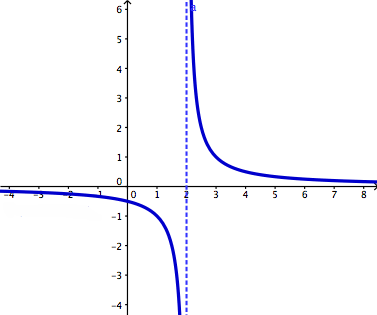
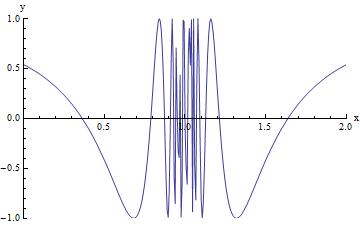
A discontinuous function is the opposite of a continuous function. It may contain breaks, holes, jumps. Also, the value does not equal the limit. There are two families of discontinuities: removable and non-removable discontinuities. In the removable family there is only point discontinuity. In removable discontinuities the limit DOES EXIST. In the other family, non-removable discontinuities the limit DOES NOT EXIST. The non-removable discontinuities family consists of jump discontinuity, oscillating behavior, and infinite discontinuity. In the jump discontinuities one hole has to be close and one open or both open or it will not be a function if both of the holes are closed. The reason the limit does not exist in jump discontinuities is because it approaches different values from the left and right. In oscillating behavior the graph is very wiggly and the limit does not exist because it doesn't approach any single value. Infinite discontinuities are caused by vertical asymptotes and the limit does not exist because of unbounded behavior (can't touch asymptotes) and because it approaches different values from the left and right. 

http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity

   

http://www.tutorvista.com/content/math/discontinuity/

http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity

http://www.cwladis.com/math301/limitsgraphically.php

2. A limit is the intended height of a function. The height is just the y-value of the function. Different x-values have different heights. A limit exists as long as you reach the same height from both the left and right. In order for a limit to exist, both the right hand limit and the left hand limit must be the same. If a graph does not break at a given x-value, a limit exists there. A limit can still exist if the destination is a hole in the graph. A graph can have an infinite amount of limits. Limits do not exist at specific points in the three non-removable discontinuities-jump, infinite, and oscillating. The limit does not exist at jump discontinuities because it approaches different values from the left and right. The limit does exist at infinite  discontinuities because of unbounded behavior (can't touch asymptotes) and it approaches different values from the left and right. The limit does exist at oscillating behavior because it does not approach any single value because infinity is not anything you can get to. The difference between a limit and a value is the actuality. A limit is the intended height, while a value is the actual height.
3.We evaluate limits numerically by typing in the given function into out y= screen in our graphing calculator. Then, pressing the graph button and then hitting the trace button and we put in the number that we given in the table and repeat for all the others. On the left side of the table the number should increase from out to inner and on the right side of the table the number should increase out to inner. Then, you write out the number that is the middle or what the numbers are approaching and that number will become the limit. After, that you just write it as limit notation. We evaluate limits graphically by putting your finger on a spot to the left and to the right of where you want to evaluate the limit. If your fingers meet up then that y-value will be you limit. If your fingers do not meet up, the limit does not exist. The possible reasons for why the limit does not exist is because different values from the left and right, unbounded behavior, and oscillating behavior.We can evaluate limits algebraically by using three different methods. The first method, is substitution which is the easiest way to go about and we should always try to see if we get a numerical value, #/0(undefined= LIMIT DNE because unbounded behavior),and 0/#(limit is zero). If we ever get 0/0 when using the substitution method that means it is indeterminate, which means not yet determined and we must use another method. The substitution method means you take the number limit is approaching and plug it anytime you see "x". The second method, is factoring we use this method when the substitution method gives us 0/0 and the numerator or denominator are factorable. When using the factoring method we factor the numerator and denominator and cancel common terms to remove the zero(hole) in the denominator and then we use direct substitution method to get the limit. The last method is the conjugate method, we use this when the substitution method gives us 0/0 and the numerator or the demoniator are not factorable. We evaluate the limit using the conjugate method by first multiplying the top and bottom by the conjugate of the numerator or denominator(we use the conjugate of the numerator/denominator depending wherever the radical is). Then we simplify by foiling(you don't multiply the non-conjugate part because you want things to cancel) and then things will cancel and then we use the substitution method.